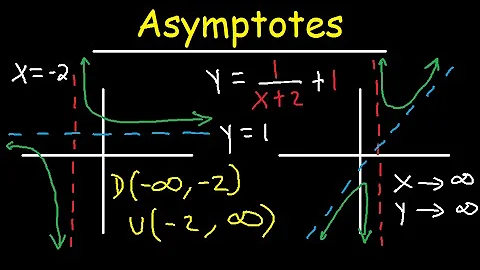
Comment trouver l’asymptote d’une fonction ?

Comment trouver l’asymptote d’une fonction ?
Une asymptote est une droite vers laquelle la fonction tend. C’est à dire que plus x va se rapprocher de la limite étudiée, plus la fonction sera presque égale à la droite « asymptote ». Pour trouver une asymptote d’une fonction il faut donc regarder comment évolue la fonction au voisinage de la limite recherchée.
Comment savoir si il y a une asymptote ?
Les asymptotes
- Elle est verticale en x=a si la limite d’une fonction f au voisinage de a tend vers l’infini et que f(a) n’existe pas (voir courbe en page logarithme). …
- Une asymptote est horizontale si la limite de la fonction à l’infini est égale à un réel.
Quand asymptote horizontale ?
1) Asymptote horizontale f(x) = l, pour M et P les points d’abscisses x, lorsque x prend des valeurs de plus en plus grandes, la distance PM tend vers 0 : On dit alors que la droite D d’équation y = l est asymptote horizontale à la courbe Cf au voisinage de +∞.
Comment trouver l’équation d’une asymptote verticale ?
Pour savoir si une fonction possède une asymptote verticale, il faut déterminer les valeurs de x qui annulent le dénominateur. donc lorsque la fonction f s′approche de 1 par la gauche,���� prend des valeurs qui tendent vers − ∞. Cela confirme aussi l’asymptote verticale en x = 1 car la condition 1 est vérifiée.
Comment trouver l’asymptote horizontale d’une fonction ?
Conclure sur l’existence d’une asymptote horizontale Si la limite trouvée est un réel a, on en déduit que la droite d’équation y = a y=a y=a est asymptote horizontale à C f C_{f} Cf en +∞. Si la limite trouvée est +∞ ou −∞, alors C f C_{f} Cf n’admet pas d’asymptote horizontale en +∞.
Comment trouver l’asymptote verticale d’une fonction ?
La droite d’équation x = a est une asymptote verticale à la courbereprésentative de la fonction f en a si et seulement si f(x) a pour limite ou lorsque x tend vers a, éventuellement seulement à droite ou à gauche de a.
Comment savoir si il y a une asymptote oblique ?
Une asymptote oblique correspond à une droite possédant une pente non nulle (il s’agirait sinon d’une asymptote horizontale) et non infinie (il s’agirait sinon d’une asymptote verticale). Tout polynôme admet une asymptote oblique si le degré du numérateur est supérieur au degré du dénominateur.
Comment savoir si une fonction à une asymptote horizontale ?
Si la limite trouvée est un réel a, on en déduit que la droite d’équation y = a y=a y=a est asymptote horizontale à C f C_{f} Cf en +∞. Si la limite trouvée est +∞ ou −∞, alors C f C_{f} Cf n’admet pas d’asymptote horizontale en +∞.
Comment savoir si l’asymptote est verticale ou horizontale ?
La droite d’équation x = a est une asymptote verticale à la courbereprésentative de la fonction f en a si et seulement si f(x) a pour limite ou lorsque x tend vers a, éventuellement seulement à droite ou à gauche de a.
Comment démontrer qu’une fonction admet une asymptote verticale ?
Si C f C_{f} Cf admet une asymptote verticale, c’est nécessairement en un réel a correspondant à une borne finie (c’est-à-dire réelle) et ouverte (c’est-à-dire exclue) du domaine de définition de f. On liste donc tous les réels a vérifiant cette condition.
What does an asymptote represent?
- An asymptote is a line that the graph of a function approaches, but never intersects. An asymptote can occur when a denominator in a function includes a variable that cannot be canceled out by something in the numerator. Horizontal asymptotes are horizontal lines that the graph of a function approaches as x tends to plus or minus infinity.
How do you find asymptote?
- To find the horizontal asymptote, one should determine the degree of both the numerator and denominator from the original function. If the degrees are the same, simply divide the first term of the numerator by the first term of the denominator.
How to write an asymptote?
- Step 1: Write f (x) in reduced form Step 2: if x – c is a factor in the denominator then x = c is the vertical asymptote. Step 2: The denominator is x – 3, and so the Vertical Asymptote is at x = 3.
What is an asymptote example?
- A common example of a vertical asymptote is the case of a rational function at a point x such that the denominator is zero and the numerator is non-zero. If a function has a vertical asymptote, then it isn’t necessarily true that the derivative of the function has a vertical asymptote at the same place.
